Mastering Binary Trees-Wahab's Blog

Overview

Binary trees are a data structure in computer science that consist of nodes with each node having at most $2$ children, referred to as left/right child. They are often used to organize data hierarchically, allowing efficient insertion, deletion and search operations. Common types of binary trees include binary search trees, where nodes are ordered such that for each node, all elements in its left subtree are less than the node’s value, and all nodes in its right subtree are greater than or equal to the node’s value.

Here is an example of a binary tree:

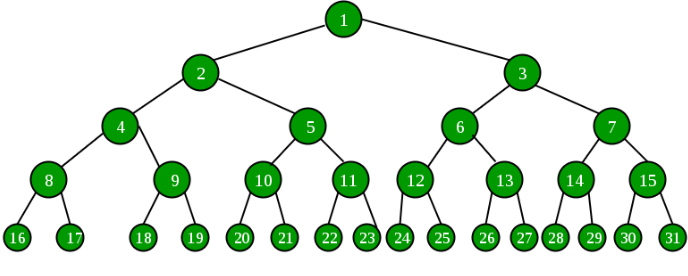
The node structure itself stores some data and stores references to left and right subtrees. It can be defined as follows:

class BinaryTreeNode:
    def __init__(self, data=None, left=None, right=None):
        self.data = data
        self.left = left
        self.right = right

Jargon

Let’s summarize common terminology often used when referring to different parts of a sub-tree:

Root: The topmost node in the tree, which does not have a parent
Parent: A node that has one or more children nodes
Child: Node that is a direct descendant of a parent node
Leaf: Node with no children
Ancestor: A node that is part of a node’s lineage, from the root to its parent, grandparent, and so on.
Descendant: A node that is part of a node’s subtree, including its children, grandchildren, and so on.
Sibling: Nodes that share the same parent.
Depth: The length of the path from a node to the root. The root has a depth of 0.
Height: The length of the longest path from a node to a leaf in its subtree. A leaf has a height of 0.
Level: The set of nodes that are the same distance (depth) from the root.
Subtree: A tree consisting of a node and its descendants.
Internal node: A node that is not a leaf, meaning it has at least one child.

Traversals

Traversal is an order in which you can visit the nodes in a tree when solving a problem. All the amount to is where you put the print statement or problem-solving logic. Here is a review:

# Time: O(n)
# Space: O(h)
# Let h be the height of the binary tree
# Let n be the number of nodes in the tree
# Binary tree is not always n = 2^h, so we must seperate the two variables above
def tree_traversal(root):
    # Preorder Traversal - process root data before traversal left and right
    print("Preorder: ", root.data)
    tree_traversal(root.left)

    # Inorder Traversal - process root data after traversing left
    print("Inorder: ", root.data)
    tree_traversal(root.right)

    # Postorder Traversal - process root data after left and right
    print("Postorder: ", root.data)

Now lets dive into how each of these traversals work with specific diagrams:

       A
     /   \
    B     C
   / \   / \
  D   E F   G

Lets start by analyzing preorder traversl, so in simple words print data before left/right traversal:

A -> B -> D -> E -> C -> F -> G

Next, we do inorder traversal, so traverse left, print, then print right:

D -> B -> E -> A -> F -> C -> G

Next, we do postorder traversal, so traverse left, then right and then print:

D -> E -> B -> F -> G -> C -> A

Ex: Balanced Tree

A binary tree is said to be height balanced if for each node the difference between left and right subtrees is at most one. Here is an example of a non-perfect binary tree:

        A
      /   \
     B     C
    / \   /
   D   E F
  / \
 H   I

If we start by thinking about the brute force approach, we can solve this question if we have a way to find the height for every node. So, we for every node we compute the height of the left and right subtree and check if they are balanced we return true otherwise we return false. We do this for all nodes.

# Let n be number of nodes
# Time: O(n) - The helper can traverse all nodes in a tree in the worst case
# Space: O(n) - The height of a tree in the worst case is also n, so n stack height
def height_helper(tree):
    Basecase if no tree exists the height is 0
    if tree is None: return 0
    return 1 + max(height(tree.left), height(tree.right))

# Time: O(n^2) - DFS traverses all nodes, at each node we call height_helper
# Space: O(n) - In the worst case the depth can be as deep as the number of nodes
def is_balanced_binary_tree(tree):
    # Basecase - Empty tree is height balanced
    if tree is None: return True

    # Compute left and right heights
    left_height = height_helper(tree.left)
    right_height = height_helper(tree.right)

    # Check if current subtree is balanced
    if abs(left_height - right_height) > 1:
        return False

    # Check if all subtrees are balanced
    return is_balanced_binary_tree(tree.left) and \
           is balanced_binary_tree(tree.right)

We very quickly note that we are making duplicate calls to height_helper from is_balanced_binary_tree so a quick an quite effective optimization we can make is to cache function calls to height_helper so we don’t duplicate computation.

# Let n be number of nodes
# Time: O(n) - The helper can traverse all nodes in a tree in the worst case
# Space: O(n) - The height of a tree in the worst case is also n, so n stack height
@functools.lru_cache(None)
def height_helper(tree):
    Basecase if no tree exists the height is 0
    if tree is None: return 0
    return 1 + max(height(tree.left), height(tree.right))

# Time: O(n) - DFS traverses all nodes, at first node we call height_helper
# height helper will only be called for the first node and the results will be
# cached for the remaining nodes
# Space: O(n) - In the worst case the depth can be as deep as the number of nodes
def is_balanced_binary_tree(tree):
    # Basecase - Empty tree is height balanced
    if tree is None: return True

    # Compute left and right heights
    left_height = height_helper(tree.left)
    right_height = height_helper(tree.right)

    # Check if current subtree is balanced
    if abs(left_height - right_height) > 1:
        return False

    # Check if all subtrees are balanced
    return is_balanced_binary_tree(tree.left) and \
           is balanced_binary_tree(tree.right)

However, lets try to work though how we would optimize this function without using lru_cache. Use a bottom up approach, which eliminates the need for redundant height calculations and use tuple returns to pass height values and balance checks. Using a bottom up approach requires us to use post order traversal, so we check if the node is balaced after traversing both left and right. This ensures that we are traversing the tree bottom up and returning heights and balanced and so we don’t need redundant height calculations:

def is_balanced_binary_tree(tree):
    # Defining a custom return type to return
    # if a node is balanced and also the hight
    balancedAndHeight = collections.namedtuple(
        'balancedAndHeight', ('balanced', 'height'))

    def check_balanced(tree):
        # Basecase - Empty Tree is height balanced
        if tree is None:
            return balancedAndHeight(balanced=True, height=-1)

        # Check left and right for balanced
        left_result = check_balanced(tree.left)
        if not left_result.balanced: return False

        right_result = check_balanced(tree.right)
        if not right_result.balanced: return False

        # Check if the current node is balanced
        is_balanced = abs(left_result.height - right_result.height) <= 1
        height = max(left_result.height, right_result.height)

        return balancedAndHeight(balanced=is_balanced, height=height)

    return check_balanced(tree)

Ex: Check if a binary tree is symmetric

A tree is symmetric if you can draw a vertical line down the middle of the tree and the reflection matches the original. For example:

   Symmetric Tree            Asymmetric Tree

        1                         1
       / \                       / \
      2   2                     2   2
     / \ / \                   /     \
    3  4 4  3                 3       4

Write a program that determines if a tree is symmetric.

Now, I would like to share my very first attempt at soluving this question which in fact is INCORRECT and I will explain why:

# Time: O(n) - We need to loop through all possible nodes
# Space: O(n) - In the worst case the height is equal to all the nodes
def is_symmetric(tree):
    # Basecase
    if tree is None: return True, None

    # Check left and right subtrees
    left_symmetric, left_value = is_symmetric(tree.left)
    right_symmetric, right_value = is_symmetric(tree.right)

    return left_value == right_value and left_symmetric and right_symmetric

This solution at first glance looks right. However, there is a subtle mistake. The following tree is not symmetric however, the above code will return true:

Additionally, the following tree is symmetric but the incorrect code above will return False:

So we must re-examine, and think through a solution that accounts for the subtleties. We are not comparing each branch at every node to confirm if the left and right data is equal. Rather, we are comparing the branching from the root node to confirm symmetry exists. Now that we have that in mind, we will need two recursive functions to ensure the first function executes checking symmetry from the root node and another function that checks both left and right subtrees are mirror images of each other. In order for two subtrees to be mirror images of each other we have $4$ requirements:

If the right branch of the right tree equals the left branch of left subtree
If the left branch of the right subtree equals the right branch of the left subtree

Now with this in mind we can construct the correct optimized solution:

# Time: O(n) - we are checking all subtrees once -- Thus, we are checking all nodes once
# Space: O(n) - The stack space required is the same as the height which in the worst case is n
def is_symmetric(tree):

    def check_symmetric(left_tree, right_tree):
        # Basecase: both are None thus symmetric
        if left_tree is None and right_tree is None: return True

        # Otherwise: lets check both subtrees
        if left_tree is not None and right_tree is not None:
            return left_tree.data == right_tree.value and \
            check_symmetric(left_tree.left, right_tree.right) and \
            check_symmetric(left_tree.right, right_tree.left)
        else: return False

    return not tree or check_symmetric(tree.left, tree.right)

Ex: Compute The lowest common ancestor in a binary tree

Any $2$ nodes have several ancestors in a binary tree. The ancestor that is guranteed if any $2$ nodes is the root. In this example, we want to find an ancestor that is common to both nodes but is also the furthest ancestor from the root node.

Here is an example, the lowest common ancestor for the following binary tree is B because it is the root of the smallest possible subtree that includes both G and I nodes.

            A
         /     \
      (B)       C
     /   \       \
   D       E       F
  / \     / \     / \
(G)  H  (I)  J   K   L

Lets start off by thinking about a brute force solution. Suppose we have a function which finds if a node is in a tree, we can call this function twice for each possible subtree until we find subtree that doesn’t have both nodes, the parent of this subtree will be the lowest common ancestor.

# Time: O(n) - Essentially DFS to find nodes
# Space: O(n) - In worst case the stack space equals number ofnodes
def node_found(tree, node):
    # Basecase if root and node match then node is found
    if tree is None: return False
    if tree.data == node.data: return True

    # Search left and right subtrees
    return node_found(tree.left, node) or \
            node_found(tree.right, node)

# Time: O(n^2) - We call DFS and for each node we call node_found
# Space: O(n) - The stack height in the worst case is still n
def find_lowest_common_ancestor(tree, nodeA, nodeB):

    # Find which direction contains both nodes
    go_left = node_found(tree.left, nodeA) and \
              node_found(tree.left, nodeB)

    go_right = node_found(tree.right, nodeA) and \
                node_found(tree.right, nodeB)

    # Go lower to find the lowest common ancestor
    if go_left:
        return find_lowest_common_ancestor(tree.left, nodeA, nodeB)
    elif go_right:
        return find_lowest_common_ancestor(tree.right, nodeA, nodeB)
    else:
        # Both nodes are neither in left or right subtrees,
        # so lowest ancestor found
        return tree

Ok, lets try to optimize this algorithm now. So if we look at this algorithm carefully we see that we are essentially running Depth First Search twice. Lets now try to find how to solve this problem with a single DFS. The idea is to do bottom up depth first search which tracks at which node both target nodes meet first. Thus making it the lowest commong ancestor:

# Time: O(n) - Perform DFS once
# Space: O(n) - worst case stack height is n
def solve(tree, nodeA, nodeB):
    # Basecases
    if not tree: return False, None
    if tree.data == nodeA.data: return True, None
    if tree.data == nodeB.data: return True, None

    # Perform DFS bottom up - Post Order Traversal
    found_in_left, possibilityA = find_lowest_common_ancestor(tree.left, nodeA, nodeB)
    found_in_right, possibilityB = find_lowest_common_ancestor(tree.right, nodeA, nodeB)

    # Pass the ancestor all the way up
    if found_in_left and found_in_right:
        return True, tree
    elif possibilityA is not None:
        return True, possibilityA
    elif possibilityB is not None:
        return True, possibilityB

    # Ancestor not found
    return False, None

# Time: O(n) - We are just running solve
# Space: O(n) - We are just running solve
def find_lowest_common_ancestor(tree, nodeA, nodeB):
    _, ancestor = solve(tree, nodeA, nodeB)
    return ancestor

Ex: Compute the lowest common ancestor when nodes have parent pointer

Lets modify the structure of a node to allow a node to have a pointer to the parent. Here is the modified structure:

class BinaryTreeNode:
    def __init__(self, data=None, left=None, right=None, parent=None):
        self.data = data
        self.left = left
        self.right = right
        self.parent = parent

The question now becomes we if can come up with a even more efficient algorithm than O(n) and O(n) by simple storing a tiny field in the binary tree data structure.

Since we have the parent pointer, we do not use any stack space to find the original nodes. This is because we are given the original nodes and we don’t need to use any sort of DFS traversal to find them. Rather, we can use our knowledge of the depth of a node to find the lowest common ancestor. Recall:

Depth is the measure of how far a node is from the root of a tree

Suppose nodeA has a depth $d_1$ and nodeB has a depth $d_2$. We have the following three cases:

$$ d_2 = d_1 \ \ \ \ (1) \\ d_1 > d_2 \ \ \ \ (2) \\ d_2 > d_1 \ \ \ \ (3) \\ $$

For case $(1)$, if we find both nodes to have the same height, the first node in common when traversing up would be the lowest common ancestor.

For case $(2)$ and $(3)$, we can find the offset by computing $\text{max}(d_1,d_2) - \text{min}(d_1,d_2)$. This offset can be applied to the lower node and then we would have the solution to case $(1)$ apply to solve for the lowest common ancestor.

# Time: O(n) - We traverse the height which in the worst case is n
# Space: O(1)
def uniform_up_ancestor(nodeA, nodeB):
    while nodeA != nodeB:
        nodeA, nodeB = nodeA.parent, nodeB.parent
    return nodeA

# Time: O(n) - We traverse the height which in the worst case is n
# Space: O(1)
def depth_of(node):
    depth = 0
    while node:
        node, depth = node.parent, depth+1
    return depth

# Time: O(n) - We traverse the height which in the worst case is n
# Space: O(1)
def traverse_up(node, offset):
    while offset > 0 and node:
        node = node.parent
        offset -= 1
    return node

# Time: O(n) - Just call the helper functions
# Space: O(1) - Also just call the helper functions
def find_lowest_common_ancestor(nodeA, nodeB):
    # Compute necessary stats
    depthA = depth_of(nodeA)
    depthB = depth_of(nodeB)
    offset = abs(depthA - depthB)

    # Move nodes to equal offsets
    if depthA > depthB:
        nodeA = traverse_up(nodeA, offset)
    elif depthB > depthA:
        nodeB = traverse_up(nodeB, offset)

    # find common ancestors in uniform up direction
    return uniform_up_ancestor(nodeA, nodeB)

Ex: Sum root to leaf paths in a binary tree

If we have a binary tree where each node contains a binary digit. Write a program that computes the sum of all root to leaf binary combinations. For example:

Assuming root is the most significant bit, the solution is:

5+4+7+6

We can use in preorder traversal to accrue weighted node values and pass them to left and right children which perform the same operation recursively.

# Time: O(n) - DFS
# Space: O(n) - worst case height is n
def root_to_leaf_sum(root, current_sumi=0):
    # Basecase
    if not root: return 0

    # Update Sum
    current_sum = root.value + current_sum * 2

    if not root.left and not root.right:
        return current_sum

    # Compute remaining sums
    left_sum = root_to_leaf_sum(root.left, current_sum)
    right_sum = root_to_leaf_sum(root.right, current_sum)

    return left_sum + right_sum

Ex: Find a root to leaf path with a specified sum

Given a sum, check if there is a root to leaf path that equals to that sum. For example:

      5
     / \
    4   8
   /   / \
  11  13  4
 / \      \
7   2      1

If we are given the target sum of $22$, we can confirm that the following path matches the target sum, so we must return True.

5 -> 4 -> 11 -> 2

The structure of this problem is similar to the previous problem because both problems are in a way dealing with root to leaf sums. Additionally, we have the basecases outlined fairly well, which is does the sum at the leaf node match the target. We can use simple DFS to traverse the tree and check for the basecase:

# Time: O(n) - Performing DFS
# Space: O(n) - worst case stack height is n
def has_path_sum(tree, remaining_sum):
    # Edge Case
    if not tree: return False

    # Base Case
    if not tree.left and not tree.right:
        return remaining_sum == tree.value

    # Recursively check all nodes
    return has_path_sum(tree.left, remaining_sum - tree.value) or \
        has_path_sum(tree.right, remaining_sum - tree.value)

Ex: Implement an preorder, inorder and postorder traversal without recursion

We gave various traversals, preorder traversal, inorder traversal and postorder traversal. In this example we need to write a program that performs all possible traversals that does not use recursion.

To solve this question we must think about how recursion works. Briefly, recursion uses stack space and stacks recursive calls until we reach a basecase. If we are going to write recursion interativly we must find a way to mimic this behaviour. This means we need to leverage the stack data structure to mimic this behaviour.

Preorder Traversal

# Time: O(n) - Need to traverse all nodes n
# Space: O(n) - The stack space in the worst case is n
def interative_preorder_traversal(root):
    # Edgecase
    if not root: return

    # Use array as a stack
    stack = [root]

    while stack:
        node = stack.pop()
        print(node.value)

        # Place left last because we always need to pop left first
        if node.right: stack.push(node.right)
        if node.left: stack.push(node.left)

Inorder Traversal

# Time: O(n) - Need to traverse all nodes n
# Space: O(n) - The stack space in the worst case is n
def interative_inorder_traversal(root):
    stack = []
    current = root
    while True:
        if current is not None:
            stack.push(current)
            current = root.left
        elif stack:
            node = stack.pop()
            print(stack.value)
            current = node.right
        else:
            break

Postorder Traversal

# Time: O(n) - Need to traverse all nodes n
# Space: O(n) - The stack space in the worst case is n
def interative_postorder_traversal(root):
    if root is None: return

    stack = []
    prev = None

    while root or stack:
        while root:
            stack.push(root)
            root = root.left

        root = stack[-1]

        if root.right is None or root.right == prev:
            print(root.value)
            stack.pop()
            prev = root
            root = None
        else:
            root = root.right

Ex: Compute the k-th node in an inorder traversal

This problem is trivial given the previous recursive and iterative techniques. However, if we allow each node to store the number of nodes in its subtrees including that node, what is the most optimal way to compute the k-th node in an inorder traversal:

class BinaryTreeNode:
    def __init__(self, data=None, left=None, right=None, subnodes=None):
        self.data = data
        self.left = left
        self.right = right
        self.size = subnodes

We want to write an algorithm takes a look at the sub-tree size and decides wether the k-th nodes falls in that subtree, otherwise we can simply return and avoid exploring the subtree. We can do this iteratively by using a variant of the iterative inorder traversal. While the tree exists we can take a look at the number of subnodes and find if the kth node is in the left subtree, right subtree or the current node.

# Time: O(n)
# Space: O(1)
# Let n be the number of nodes
def find_kth_node_binary_tree(tree):
    while tree:
        left_size = tree.left.size if tree.left else 0
        if left_size+1 < k:     # The kth node is not in the left subtree
            k -= left_size + 1
            tree = tree.right
        elif left_size == k-1:  # Current node is the kth node
            return tree
        else:                   # Go to the left subtree
            tree = tree.left
    return None

Mastering Binary Trees

Contents